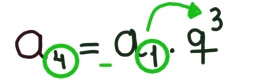Progressão geométrica: fórmula, exercícios e exemplos

Progressão geométrica é uma sequência numérica que geralmente cresce ou decresce rapidamente e em proporções elevadas.

Isso ocorre porque os termos de uma PG vão sendo multiplicados sucessivamente por um número constante, o qual denominamos de razão.

Existem inúmeros exemplos progressão geométrica ao nosso redor. Apenas para exemplificar: no ano de 2020, quando o mundo foi surpreendido e aterrorizado pela Pandemia de Covid-19, vários matemáticos e cientistas elaboraram modelos para analisar e prever o avanço do vírus com base em funções exponenciais e progressões geométricas.

Eles traçaram gráficos a partir de informações obtidas na prática, tais como o fato de uma pessoa contaminada, por exemplo, também ser capaz de contaminar outras três pessoas ou mais.

Assim, os estudiosos tentaram prever o avanço da doença conforme os modelos matemáticos propostos com base em P.G. (progressão geométrica).

Esse assunto é muito importante, sobretudo porque é muito cobrado em provas, concursos e vestibulares (incluindo o Enem), motivo pelo qual vamos estabelecer a fórmula da progressão geométrica, realizar demonstrações através de exemplos e resolver muitos exercícios sobre o tema.

Para se situar no texto, siga o índice:

{getToc} $title={Índice da aula textual}

O que é uma progressão geométrica

Antes de tudo, vamos estabelecer um conceito que seja assimilado da forma mais fácil possível.

Progressão geométrica é qualquer sequência de números não nulos, em que cada termo a partir do segundo é igual ao termo anterior multiplicado por uma constante denominada razão ou quociente.

Em outras palavras, PG é uma sequência de números em que o resultado da divisão de determinado termo pelo termo antecedente é sempre constante (razão).

Na prática, as progressões geométricas são construídas a partir de um termo específico, o qual será multiplicado por um número constante, ou seja, a razão, a fim de se formar o termo posterior e assim sucessivamente.

Imagine uma escada hipotética, onde os degraus vão aumentando de tamanho. Quanto mais alto o degrau, maior será o seu tamanho. Essa viagem mental nos ajudará a entender o que é progressão geométrica, para além de seu conceito meramente teórico.

Exemplos de progressão geométrica

Para facilitar o entendimento do conceito observado acima, veremos a seguir alguns exemplos de progressão geométrica:

👉 (2, 4, 8, 16, 32, 64)

Podemos notar nesse exemplo de progressão geométrica que os números crescem com base na operação de multiplicação.

Temos o primeiro, segundo, terceiro, quarto, quinto e sexto termos. Note que se trata de uma PG finita, pois o número de termos está limitado a seis. Contudo, também existem as progressões geométricas infinitas, cujos termos são ilimitados.

Vamos agora nomear os termos da nossa PG.

• Primeiro termo: a₁ = 2
• Segundo termo: a₂ = 4
• Terceiro termo: a₃ = 8
• Quarto termo: a₄ = 16
• Quinto termo: a₅ = 32
• Sexto termo: a₆ = 64

Note que os termos foram crescendo à medida em que foram multiplicado por dois:

2 × 2 = 4

4 x 2 = 8

8 x 2 = 16

...

Isto é, os termos são sucessivamente multiplicados pela razão da PG, que é 2.

Sempre que quisermos saber o valor da razão ou quociente, basta realizarmos a divisão de determinado termo pelo seu termo anterior. Por exemplo:

4 ÷ 2 = 2

8 ÷ 4 = 2

16 ÷ 8 = 2

...

Essa informação nos ajudará a construir a fórmula da progressão geométrica, também conhecida como termo geral da PG.

Também é importante destacarmos que, de acordo com o valor da razão, uma progressão geométrica pode ser classificada como crescente, constante, decrescente ou alternada, conforme vamos conferir abaixo.

Progressão geométrica crescente

Uma progressão geométrica é crescente quando sua razão, que chamaremos simplesmente de q, é maior que 1.

Matematicamente, podemos afirmar que q > 1.

Por exemplo:

👉 1, 3, 9, 27, 81, ...

Para calcularmos a razão da PG supracitada (citada acima), devemos dividir determinado termo dela pelo termo antecedente, conforme demonstrado a seguir:

3 ÷ 1 = 3

9 ÷ 3 = 3

27 ÷ 9 = 3

...

Já deu para perceber que a razão da PG é 3, ou seja, maior que um, motivo pelo qual temos então uma progressão geométrica crescente, onde seus termos crescem numericamente conforme ela vai se desenvolvendo.

Progressão geométrica constante

Uma progressão geométrica será constante quando sua razão for exatamente igual a 1. 

Matematicamente: q = 1. Simples assim!

Vejamos um exemplo:

👉 3, 3, 3, 3, 3, 3, ...

Observe que todos os termos da progressão geométrica constante são idênticos. 

Isto decorre da propriedade do elemento neutro da multiplicação, a qual garante que existe um número que, ao ser multiplicado por qualquer outro número, não o altera. Esse número é o 1, também chamado de elemento neutro da multiplicação. 

Em outras palavras, qualquer número será ele mesmo quando multiplicado por 1. Esse é o singelo motivo pelo qual os termos da PG de razão 1 serão sempre iguais (por exemplo: 3x1=3, 3x1=3, 3x1=3, ...).

Progressão geométrica decrescente

Teremos uma progressão geométrica decrescente quando a sua razão corresponder a um número maior que zero e menor que um, ou seja, a razão ou quociente será um número fracionário.

Em linguagem matemática, podemos escrever: 0 < q < 1.

Vamos conferir mais um exemplo:

É possível observamos que, nesta PG, os termos estão diminuindo numericamente conforme a progressão se desenvolve.

Isto ocorre porque a razão da PG é um meio (1/2), que logicamente é maio que 0 e menor que 1.

Em outras palavras, cada termo é multiplicado pelo quociente 1/2, gerando o termo posterior que equivale à metade do termo anterior.

Progressão geométrica alternada ou oscilante

Será alternada ou oscilante a progressão geométrica que possui razão negativa, ou seja, menor que zero: q < 0.

Preste atenção aos números positivos (em azul) e negativos (em vermelho) se alternando na PG:

Olhando rapidamente para esta PG, podemos notar claramente que os termos estão oscilando ou se alternado entre valores positivos e negativos.

Esse fenômeno ocorre porque a razão possui valor negativo (-2), ou seja, menor que 0.

Veja como a progressão é formada:

1 x (-2) = -2

(-2) x (-2) = 4

4 x (-2) = -8

(-8) x (-2) = 16

...

Fórmula da progressão geométrica

Depois de elaborado o conceito e após a visualização de alguns exemplos, vamos aprender como é construída a fórmula da progressão geométrica, também conhecida como termo geral da PG.

Veja a progressão geométrica adiante:

👉 1, 4, 16, 64, 256...

Ela se inicia com o termo numérico 1, o qual é multiplicado por 4, criando o segundo termo. 

O segundo termo, por sua vez, também é multiplicado por 4, gerando o terceiro termo e assim sucessivamente.

Fazendo de outra forma, podemos calcular de imediato a razão da PG, dividindo um termo pelo seu termo imediatamente anterior. 

Por exemplo: 4 ÷ 1 = 4; 16 ÷ 4 = 4; 64 ÷ 16 = 4.

A razão q é constante. Na presente hipótese, q = 4.

Vamos esquematizar os cálculos que formam esta PG da seguinte maneira:

a₁ = 1

a₂ = a₁ x q = 1 x 4 = 4

a₃ = a₂ x q  = 4 x 4 = 16

a₄ = a₃ x q  = 16 x 4 = 64

a₅ = a₄ x q  = 64 x 4 = 256

Acabamos de verificar a construção da progressão geométrica através da multiplicação de cada um dos seus termos pela razão.
No entanto, também é possível construirmos a PG tão somente a partir do primeiro termo e da razão.

Comprovaremos isso na prática! Olhe:

a₁ = 1

a₂ = a₁ x q = 1 x 4 = 4

a₃ = a₁ x q x q = 1x 4 x 4 = 16

a₄ = a₁ x q x q x q = 1 x 4 x 4 x 4 = 64

a₅ = a₄ x q x q x q x q = 1 x 4 x 4 x 4 x 4 = 256

Preste bastante atenção e irá perceber que, a partir do primeiro termo, é possível montarmos a progressão geométrica se nós multiplicarmos uma vez a mais a razão em relação ao termo anterior.
Veja por exemplo que:

a₂ = a₁ x q

a₃ = a₁ x q x q ou a₃ = a₁ x q²

Ou seja, se quisermos descobrir o valor de a₃ a partir de a₁, basta multiplicarmos a razão duas vezes em relação ao primeiro termo (como se subíssemos dois degraus de uma escada em que cada degrau corresponde a uma razão).

Avançando... se quiséssemos saber o valor o quarto termo (a₄), teríamos que partir do primeiro degrau e avançar mais 3 passos, que correspondem a razão q. Matematicamente, fica da seguinte forma:

a₂ = a₁ x q

a₃ = a₁ x q x q ou a₃ = a₁ x q²

a₄ = a₁ x q x q x q ou a₃ = a₁ x q³

👀 Apenas para relembrar as regras de potenciação: quando determinado número é multiplicado por ele mesmo várias vezes, nós podemos abreviar a multiplicação usando apenas a regra de potenciação. Por exemplo: 3 x 3 x 3 x 3 x 3 pode ser escrito de um jeito abreviado, qual seja: 3⁵ (lê-se: três elevado a cinco ou à quinta potência).

Visualize atentamente os números descritos na progressão para descobrir um fato muito importante: o valor que acompanha a razão q (número em forma de potência) é uma unidade menor que o número que acompanha o primeiro a da equação. Se ainda não conseguiu ver claramente isso, observe as imagens para facilitar a sua compreensão:

Termo geral da PG

Você acabou de ver exemplos de progressões geométricas que contêm números. Porém, podemos escrever uma PG hipotética formada apenas com letras.

Na nossa hipótese, iremos estabelecer que n é o número de termos da PG, assim como chamaremos um termo genérico de enésimo termo ou a índice n (a_n). 

Ao primeiro termo vamos atribuir o já conhecido a índice um (a₁) e a razão será representada por q. 

Seguindo a mesma lógica dos exemplos anteriores (vide imagens), o termo geral da PG hipotética é o seguinte:

A fórmula da progressão geométrica é obtida através do mesmo raciocínio de entes: o valor que acompanha a razão q será uma unidade menor que o valor que acompanha o primeiro a do termo geral da PG, ou seja, o enésimo termo.

Também é possível estabelecermos o termo geral estendido, em que os cálculos podem ser efetivados a partir de qualquer termo diferente do primeiro. 

Para isso, basta substituir 1 por k, transformando primeiro termo em k-ésimo termo. 

A fórmula estendida encontra-se disposta da seguinte maneira:

Soma dos termos de uma PG

Verifique a progressão geométrica finita a seguir:

👉 1, 5, 25, 125, 625, 3125, 15625, 78125.

Agora imagine que alguém chega para você e pede a soma de todos os termos da PG de forma rápida e objetiva.

Note que a progressão geométrica possui apenas oito termos. Mas os valores dos termos cresceram subitamente, dificultando o cálculo rápido do somatório dos termos. Mentalize por exemplo uma PG de 50 termos e que você tivesse que somar tudo? Seria um esforço hercúleo!

A boa notícia é que não precisamos fazer a soma de termos manualmente, pois existe uma fórmula para isso!

Eis que surge a salvação do estudante de progressão geométrica:

Onde:

• S_n é a soma de todos os termos
• n é o número total de termos
• a₁ é o primeiro termo
• q é a razão

É possível demonstrarmos a forma pela qual se chega à fórmula soma PG, porém o processo é um pouco mais longo e estenderia demasiadamente esta textoaula de matemática. Por isso, sugerimos no presente momento que você memorize e se familiarize com a fórmula.

Propriedades das progressões geométricas

Estamos quase concluindo a nossa abordagem teórica acerca do tema em foco. Iremos finalizar a teoria com as duas principais propriedades da progressão geométrica. 

Depois disso, passaremos à resolução de exercícios com os comentários pertinentes.

Propriedade PG #01

A primeira propriedade assegura que, em qualquer progressão geométrica, o valor de um termo corresponde justamente à média geométrica dos termos imediatamente anterior e posterior a ele.

Tomemos como base uma PG hipotética formada exclusivamente pelas letras a, b, c, d, e, f, g.

Em relação ao termo b, o termo a é anterior e o termo c é posterior. Então a propriedade garante que b² = a x c.

A mesma lógica se aplica aos demais termos. Por exemplo: d² = c x e.

Vejamos uma PG numérica para comprovarmos esta propriedade:

Observe que o quarto termo da progressão é o número oito. O terceiro termo (número 4) é o anterior e o quinto termo (número 16) é o posterior ao 8.

A médica geométrica é extraída pela raiz quadrada do resultado obtido pela multiplicação dos termos anterior e posterior (4 x 16 = 64). A raiz quadrada de 64 é exatamente 8, que é a média geométrica requerida.

Propriedade PG #02

A segunda propriedade garante que o produto dos termos equidistantes dos extremos de uma progressão geométrica é constante.

Novamente, pensemos em uma PG estruturada somente com letras do nosso alfabeto: a, b, c, d, e, f, g.

A propriedade em evidência nos assegura que a multiplicação de termos posicionados igualmente em relação aos termos extremos será sempre a mesma.

Os extremos da PG são as pontas, ou seja, o início e fim.

Por sua vez, os equidistantes dos extremos são aqueles que se posicionam a um mesma distância respectivamente do início e do fim da progressão.

Visualize os exemplos de PG com letras. A propriedade diz então que o produto dos termos equidistantes dos extremos de uma progressão geométrica é permanentemente constante. Em outras palavras: a x g = b x f ou então c x d = b x e.

Vejamos agora mesmo isso na prática:

Dá para perceber facilmente que os números 1 e 64 são os extremos. Em relação a eles, temos os termos equidistantes 2 e 32, pois o 2 está imediatamente próximo ao 1 (extremo) e o 32 está imediatamente próximo ao 64 (extremo). Do mesmo jeito, o 4 está posicionado em relação ao 1 de forma idêntica à que o 16 está em relação ao 64.

Por isso, os termos referidos são denominados equidistantes (equi- significa idêntico, igual) tendo em vista que apresentam a mesma distância em relação aos extremos da progressão geométrica.

Os cálculos confirmam o que diz a propriedade: o produto dos termos equidistantes dos extremos de uma progressão geométrica é constante.

Foi cabalmente constatado que todas as multiplicações envolvendo os termos equidistantes resultaram no numeral 64.

Progressão geométrica exercícios

Prezado(a) estudante, para sermos mais inclusivos ainda, prezadx estudante, após uma longa e detalhada exposição teórica, chegou a hora de praticarmos.

Iremos resolver muitos exercícios de PG, a fim de fixarmos o aprendizado com mais eficiência.

Consideramos mais útil abordarmos este tópico através de questões de concursos públicos e do Exame Nacional do Ensino Médio (Enem). 

Todos os exercícios são comentados e apresentam o gabarito oficial divulgado pela respectiva banca examinadora responsável pelo certame no qual foi cobrado o assunto em foco.

Exercícios de PG #01

(Prefeitura de Goioerê - PR - FAUEL - 2018 - Advogado) Considere a seguinte sequência:

3,6,9,12,15,18,21 e 24.

Quais termos devem ser removidos para que essa sequência se torne uma progressão geométrica, de razão 2 e termo inicial 3?

a) 3, 6, 12 e 21.

b) 15,18 e 21.

c) 6, 15 e 24. 

d) 9, 15, 18 e 21.

Comentários!

Observando-se a sequência numérica disposta no exercício, é possível constatarmos que se trata de uma progressão aritmética de razão 3.

⇾ Falando em progressão aritmética, se você ainda não conferiu nossa aula textual correspondente, recomendamos que acesse: Progressão aritmética: fórmula, exercícios e exemplos

No entanto, se retirarmos alguns números desta PA, ela se transforma em uma progressão geométrica de razão 2, tendo como primeiro termo o número 3.

Para resolver mais rapidamente a questão, basta estabelecer desde já uma progressão geométrica com os parâmetros solicitados (a₁ = 3 e q = 2). Vamos lá!

👉 3, 6, 12, 24

Agora vamos observar novamente a sequência estabelecida no problema e destacar apenas os números constantes na PG:

3,6,9,12,15,18,21,24.

Somente os números em negrito compõem uma PG. Os demais devem ser removidos, pois estão apenas atrapalhando a sequência geométrica.

Logo, devem ser retirados da sequência em xeque os seguintes números: 9, 15, 18 e 21, o que corresponde à alternativa d.

Portanto, gabarito: letra d.

Exercícios de PG #02

(Creative Group - 2021 - Prefeitura de Jequitibá - MG - Assistente Social) A sequência numérica (15, 30, 60, 120, 240, 480) é uma Progressão:

a) Aritmética de razão 2.

b) Aritmética de razão 4.

c) Aritmética de razão 6.

d) Geométrica de razão 2. 

Comentários!

Uma maneira bastante simples de descobrirmos se determinada sequência numérica se trata de uma PA ou PG é calcularmos o valor da razão.

Em uma PA, o valor da razão resulta da subtração de determinado termo pelo termo imediatamente anterior. O valor da razão deve ser constante, ou seja, a subtração de quaisquer termos pelo antecedente deve resultar precisamente no mesmo valor.

Então vejamos se a sequência é uma PA:

r = a₂ - a₁ = 30 - 15 = 15

r = a₃ - a₂ = 60 - 30 = 30

Opa! O valor de r não está constante, pois a subtração do segundo pelo primeiro termo resultou em 15 e a subtração do terceiro termo pelo segundo resultou em 30.

Isso comprova que a sequência não é uma PA, eliminando os itens a, b e c.

Por eliminação, a resposta correta só pode ser a letra d. Contudo, vamos comprovar o resultado.

A razão de uma progressão geométrica é obtida pela divisão de um termo pelo termo antecedente. Vamos calcular!

q = a₂ ÷ a₁ = 30 ÷ 15 = 2

q = a₃ ÷ a₂ = 60 ÷ 30 = 2

Agora sim! O valor da razão permaneceu constante, levando-nos à conclusão de que a sequência analisada se trata indubitavelmente de uma progressão geométrica de razão q = 2. Observe que os números estão dobrando de valor conforme se desenvolvem.

Portanto, o gabarito buscado é a letra d.

Exercícios de PG #03

(UniFil - 2021 - Prefeitura de Marechal Cândido Rondon - PR - Arquiteto) Considerando a Progressão Geométrica {3, 9, 27, ...}, assinale a alternativa que representa o valor do oitavo termo desta PG. OBS: Considerar (a1=3, a2=9 e a3=27)

a) 6561

b) 6601

c) 6709

d) 6830

Comentários!

Vamos resolver este exercício através da fórmula da progressão geométrica, popularmente conhecida como termo geral da PG.

Mas antes devemos descobrir o valor da razão q:

q = a₂ ÷ a₁ = 9 ÷ 3 = 3

A questão de concurso requer o valor do oitavo termo da PG, isto é, o a₈. A partir de agora, basta substituir os valores das incógnitas pelos números conhecidos e calcular:

a_n = a₁ . q^n-1

a₈ = a₁ . q^8-1

a₈ = 3 . 3⁷

a₈ = 3 . 3⁷

a₈ = 3 . 2187

a₈ = 6561

Obtivemos assim o resultado pretendido: o valor do oitavo termo da PG é 6561.

Portanto, o gabarito é a letra a, visto que é a única alternativa correta.

Exercícios de PG #04

(ENEM Prova: INEP - 2021 - ENEM - Exame Nacional do Ensino Médio) O artista gráfico holandês Maurits Cornelius Escher criou belíssimas obras nas quais as imagens se repetiam, com diferentes tamanhos, induzindo ao raciocínio de repetição infinita das imagens. Inspirado por ele, um artista fez um rascunho de uma obra na qual propunha a ideia de construção de uma sequência de infinitos quadrados, cada vez menores, uns sob os outros, conforme indicado na figura.

O quadrado PRST, com lado de medida 1, é o ponto de partida. O segundo quadrado é construído sob ele tomando-se o ponto médio da base do quadrado anterior e criando-se um novo quadrado, cujo lado corresponde à metade dessa base. Essa sequência de construção se repete recursivamente.

Qual é a medida do lado do centésimo quadrado construído de acordo com esse padrão?

a) (1/2)100

b) (1/2)99

c) (1/2)97

d) (1/2)-98

e) (1/2)-99

Comentários!

É até previsível a cena: o aluno está lá no meio da prova quilométrica do ENEM, cansado e  em uma tensão enorme, mas ainda aparece uma questão dessas. Inevitavelmente ele pensa: maldito Cornelius!

Porém...se o estudante manja de progressão geométrica, ele pensa: tô de boa na lagoa!

A questão pode ser facilmente solucionada através do termo geral da PG. 

Isso porque, avaliando a figura fornecida, vemos que os lados dos quadrados estão diminuindo pela metade uns em relação aos outros.

Vamos esquematizar as medidas dos lados de cada quadrado?

• Primeiro quadrado → 1
• Segundo quadrado → 1/2
• Terceiro quadrado → 1/4
• Centésimo quadrado → ?

Notou algo familiar nas medidas apresentadas?

Isso mesmo! Os lados do quadrado formam uma progressão geométrica decrescente. E mais: a razão da PG é 1/2 (basta dividir 1/2 por 1 para comprovar).

O primeiro termo (a₁) é justamente a medida 1.

Agora vamos dar a César o que é de César: fornecer a medida do lado do centésimo quadrado construído de acordo com esse padrão, ou seja, o a₁₀₀, conforme solicitado.

Retomando a fórmula da progressão geométrica:

a_n = a₁ . q^n-1

a₁₀₀ = a₁ . q^100-1

a₁₀₀ = 1 . (1/2)⁹⁹

a₁₀₀ = (1/2)⁹⁹

Se o candidato tivesse o domínio necessário sobre PG, ele teria resolvido essa questão de uma forma bem tranquila. Porém, se ele não houver aplicado esses conhecimentos, com certeza pode ter batido aquele desespero.

O centésimo termo da PG é (1/2)⁹⁹. 

Portanto, gabarito: letra b.

Exercícios de PG #05

(INEP - 2018 - ENEM - Exame Nacional do Ensino Médio - Primeiro e Segundo Dia - PPL) Alguns modelos de rádios automotivos estão protegidos por um código de segurança. Para ativar o sistema de áudio, deve-se digitar o código secreto composto por quatro algarismos. No primeiro caso de erro na digitação, a pessoa deve esperar 60 segundos para digitar o código novamente. O tempo de espera duplica, em relação ao tempo de espera anterior, a cada digitação errada. Uma pessoa conseguiu ativar o rádio somente na quarta tentativa, sendo de 30 segundos o tempo gasto para digitação do código secreto a cada tentativa. Nos casos da digitação incorreta, ela iniciou a nova tentativa imediatamente após a liberação do sistema de espera.

O tempo total, em segundo, gasto por essa pessoa para ativar o rádio foi igual a

a) 300.

b) 420.

c) 540.

d) 660.

e) 1 020.

Comentários!

Essa é uma das questões em que as fórmulas mais atrapalham do que ajudam. Para comprovar isso, vamos resolvê-la sem fórmula alguma.

Depois, vamos solucioná-la por meio das fórmulas da PG e da PA. Às vezes, precisamos de um pouco de sorte para sabermos qual o melhor caminho para resolver um exercício, principalmente em se tratando de matemática.

O primeiro e um dos mais importantes passos aqui é interpretar o que a questão nos diz:

👉 Primeiro erro na digitação: a pessoa deve esperar 60 segundos para digitar o código novamente.

👉 A cada digitação errada, o tempo de espera duplica, em relação ao tempo de espera anterior.

👉 Tempo gasto para digitação do código a cada tentativa: 30 segundos.

Perceba que existem tempos distintos: o tempo para digitar os códigos e o tempo de espera após um erro de digitação.

Esses dados já são suficientes para chegarmos à resposta certa. Esquematizando:

Primeira tentativa ➡ 30 segundos (errou o código)

Tempo de espera ➡ 60 segundos

Segunda tentativa ➡ 30 segundos (errou o código)

Tempo de espera ➡ 120 segundos (dobro do tempo anterior)

Terceira tentativa ➡ 30 segundos (errou o código)

Tempo de espera ➡ 240 segundos (dobro do tempo anterior)

Terceira tentativa ➡ 30 segundos (acertou o código)

Agora basta realizar uma adição simples e chegaremos ao resultado almejado: 

👉 30+60+30+120+30+240+30 = 540 segundos.

 

Essa foi a maneira mais lógica de se resolver essa questão do Enem.

Agora vamos resolver o exercício através da matemática pura, com base em progressões geométricas e aritméticas.

Inicialmente, repare que a pessoa somente conseguiu acertar o código na quarta tentativa. Assim, ele teve que enfrentar três tempos de espera consecutivos. Portanto, a PG relativa ao tempo de espera possui três termos.

O tempo de espera, neste caso, dobra a cada tentativa, significando que essa "dobra" é a razão da progressão geométrica. Em outras palavras, q = 2.

Já sabemos que a primeira tentativa corresponde a 60 segundos, este é o primeiro termo da PG.

Vamos organizar as informações:

• n = 3
• a₁ = 60
• q = 2

Diante de todos esses dados, usaremos a fórmula do somatório dos termos da PG:

s_n = a₁ x (qⁿ - 1)/q - 1

s_n = 60 x (2³ - 1)/2 - 1

s_n = 60 x (8 - 1)/1

s_n = 60 x 7

s_n = 420

Aí você pode estar pensando: tá mas a resposta foi diferente! Se pensou isso, tenha calma porque ainda não terminamos os cálculos.

Fizemos a soma dos termos da progressão geométrica referente ao tempo de espera após os erros de digitação do código do aparelho de som.

Entretanto, ainda resta somarmos o tempo reservado cada tentativa, que corresponde a 30 segundos para cada uma delas. Relembre que a pessoa tentou quatro vezes, tendo em vista que ela acertou na quarta tentativa.

Neste caso, temos uma progressão aritmética constante, com razão igual a zero, pois a cada tentativa o tempo para digitar o código não muda. Isso quer dizer que todos os termos da PA sempre serão iguais a 30.

Como a pessoa conseguiu acertar o código na quarta tentativa, temos uma PA de 4 termos.

Organizando os dados:

• n = 4
• a₁ = 30
• a₄ = 30
• r = 0

Destarte, basta usar a fórmula do somatório geral da PA:

s_n = (a₁ + a_n)xn/2

s_n = (30 + 30)x4/2

s_n = 60x2

s_n = 120

Agora sim! Vamos realizar a adição do somatório da PG referente ao tempo de espera após a digitação incorreta com o somatório do tempo reservado para cada tentativa.

Tempo total = 420 + 120

Tempo total = 540

Conclui-se que o tempo total gasto pela pessoa para ativar o rádio foi igual a 540 segundos.

Portanto, gabarito: letra c.

Viu como as fórmulas deram mais trabalho do que o raciocínio manual? Fazer o quê?! É a vida!

Esperamos que você tenha apreciado o nosso conteúdo (progressão geométrica: fórmula, exercícios e exemplos). Até a próxima, avante! Bons estudos!!!