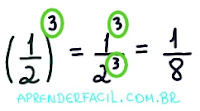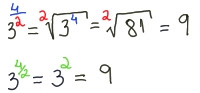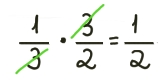Em um conceito bem simples, podemos dizer que a potenciação, também conhecida como exponenciação, é uma multiplicação na qual todos os números a serem multiplicados são exatamente iguais. Em outros termos, podemos afirmar a potenciação representa a multiplicação de um número por ele mesmo.
Então, sempre que quisermos descobrir quantos quadrados menores integram o quadrado maior, basta multiplicarmos as duas dimensões do quadrado maior, ou seja, o valor do lado do quadrado maior multiplicado por ele mesmo (base x altura).
Neste caso, para descobrirmos quantos cubinhos existem em cada cubo maior, deveremos multiplicar uma de suas arestas por ela mesma três vezes: lado x lado x lado = lado3. Isso corresponde às 3 dimensões: largura, altura e comprimento.
O número à esquerda é uma potência de potência, cuja solução conforme a propriedade correlata é efetivada por meio da multiplicação de seus expoentes, conservando-se a base:
Por exemplo: 2 x 2 x 2 x 2 x 2.
Cada um desses números é chamado de fator. No exemplo visto, cada fator é o número 2.
Ao invés de representarmos a multiplicação da maneira em que ela se encontra, simplesmente escrevemos: 2 elevado a 5 ou à quinta potência.
Isso quer dizer que, em vez de escrevermos: 2 x 2 x 2 x 2 x 2 = 32, bastaria representarmos o cálculo da seguinte forma: 25.
Apenas para ilustrar esse processo, vamos nos lembrar da operação aritmética de adição (conhecida popularmente como soma).
Na adição, podemos somar várias vezes o mesmo número. Por exemplo: 3 + 3 + 3 + 3 + 3.
Esse somatório de exemplo resulta em 15.
Porém, é possível realizarmos esse cálculo bem mais rapidamente.
Como o 3 é somado 5 vezes, basta multiplicarmos 3 por 5 e chegaremos ao mesmo resultado 15.
Ou seja, ao invés de escrevermos:
3 + 3 + 3 + 3 + 3 = 15
Podemos escrever simplesmente:
5 x 3 = 15.
Em razão disso, podemos afirmar que uma multiplicação também é uma adição.
Da mesma forma, uma potenciação também é uma multiplicação.
Mas podemos nos perguntar: qual a importância disso?
A relevância de saber potenciação reside sobretudo na praticidade que ela oferece, principalmente quando estamos realizando cálculos com número grandes.
E também não podemos esquecer que se trata de um tema constantemente cobrado em provas de concursos, vestibulares e do Exame Nacional do Ensino Médio (Enem).
Por todo o exposto nessa introdução ao conteúdo, faz-se necessário enfrentarmos o tema detalhadamente, inclusive ilustrando-o com bastantes exemplos práticos, assim como por meio de exercícios comentados e com gabarito oficial das bancas examinadoras responsáveis pela produção das provas.
Também será essencial aprendermos as propriedades da potenciação, pois elas nos ajudarão a calcular números enormes mais facilmente.
{getToc} $title={Índice da aula textual}
O que é potenciação
Potenciação, conforme já foi mencionado, é a operação matemática em que determinado número (chamado de fator) é multiplicado por ele mesmo várias vezes. Tal operação é empregada para descrever resumidamente e facilitar cálculos que envolvem a multiplicação de números muito grandes.
Vimos alguns exemplos no início da explanação e percebemos que os cálculos envolveram somente números (por ex.: 2 . 2 . 2 . 2 . 2 = 25)
No entanto, também podemos representar a potenciação de forma genérica, por meio de letras. Confira a seguir!
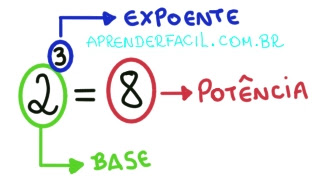
Representação:
a . a . a . a ... = an
A "fórmula da potenciação" estabelece que, se multiplicarmos o fator a por ele mesmo n vezes, o resultado será equivalente a a elevado a n.
Rescrevendo:
an = a . a . a . a ...
Onde:
a é chamado de base;
n é denominado expoente.
O resultado da operação de potenciação é denominado potência.
E n é o número de vezes que o fator será multiplicado para a obtenção do resultado. Por exemplo: 23 é igual a 8 porque o numeral 2 foi multiplicado por ele mesmo três vezes: 2 . 2 . 2 = 8.
Exemplos de potenciação
Agora vamos conferir os conceitos básicos aplicados a alguns casos práticos.
Depois dos exemplos iremos abordar as propriedades da potenciação, que são muitas e por isso exigem muita concentração de você estudante.
2 elevado a 3
Retomaremos o exemplo prático que foi recentemente mencionado: 2 elevado a 3.
Preste bastante atenção aos nomes até memorizá-los completamente: 2 é a base porque está embaixo e 3 é o expoente porque está elevado.
Perceba que a nomenclatura aplicada à matemática básica nos ajuda a entender os conceitos das operações com as quais iremos trabalhar daqui para frente.
Assim temos que 2 elevado a 3 pode ser escrito matematicamente desta forma:
👉 23
Como vimos, 2 é a base e 3 é o expoente.
A representação estabelece que o número 2 deve ser multiplicado por ele mesmo 3 vezes.
Isto é: 2 . 2 . 2 = 8.
Portanto, o resultado da potência pode ser observado:
👉 23 = 8.
2 elevado a 5
Vamos retomar o nosso exemplo inicial: dois elevado a cinco ou à quinta potência.
Matematicamente:
👉 25
Temos o número 2 embaixo e o numero 5 em cima, ou seja, em posição mais elevada.
Por esse motivo, nós chamamos o 2 de base e o 5, que está elevado, de expoente. Lemos esses números das seguintes formas: dois elevado a quinta potência ou simplesmente dois elevado a cinco, onde
2 é a base e 5 é o expoente.
Isso significa que o número 2 deve ser multiplicado por ele mesmo 5 vezes. Acompanhe novamente:
2 . 2 . 2 . 2 . 2 = 32
Logo...
25 = 32
Veremos através das propriedades que será bem mais fácil calcular os números grandes em forma de potência, sem precisar fazer essas multiplicações repetitivas.
Número elevado ao quadrado
Você já deve ter ouvido falar que determinado número estava elevado ao quadrado, significando que esse número estava submetido à segunda potência.
Convencionou-se dizer que um algarismo está elevado ao quadrado quando a referida base está elevada a 2 em homenagem às duas dimensões do chamado quadrado perfeito.
Isto é, todo número multiplicado por ele mesmo corresponde à área de um quadrado.
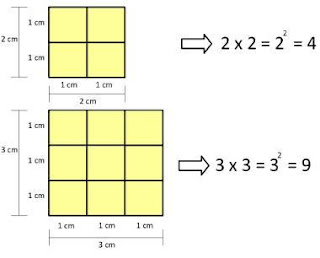
Observe a figura abaixo:
Então, sempre que quisermos descobrir quantos quadrados menores integram o quadrado maior, basta multiplicarmos as duas dimensões do quadrado maior, ou seja, o valor do lado do quadrado maior multiplicado por ele mesmo (base x altura).
O lado do quadrado maior mede 3 cm. Assim, multiplica-se lado x lado: 3 x 3 = 32. Recapitulando: no estudo da geometria plana, esse cálculo é empregado para se desvendar a área de um quadrado.
Número elevado ao cubo
Por sua vez, dizemos que determinado número está elevado ao cubo quando seu expoente é igual a 3.
Essa representação se dá em razão das três dimensões do cubo (imagine um cubo mágico).
Significa dizer que todo número multiplicado por ele mesmo três vezes corresponde precisamente ao volume de um cubo.
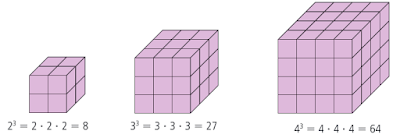
Acompanhe na ilustração:
Neste caso, para descobrirmos quantos cubinhos existem em cada cubo maior, deveremos multiplicar uma de suas arestas por ela mesma três vezes: lado x lado x lado = lado3. Isso corresponde às 3 dimensões: largura, altura e comprimento.
Desta feita, na geometria espacial, esse cálculo serve para se calcular o volume de um cubo.
Propriedades da potenciação
Depois de vistos os conceitos iniciais sobre o assunto em foco, chegou a hora de aprendermos as propriedades da potenciação. Esse assunto é de extrema importância porque envolve os cálculos de números grandes em forma potência.
Em outras palavras, ao invés de multiplicarmos as bases elevados a expoentes, vamos realizar cálculos que envolvem diretamente os próprios expoentes, conservando-se ou não as bases.
Vejamos então as propriedades mais relevantes.
Produto de potências de bases iguais
Iniciaremos com uma das propriedades mais simples, a qual é popularmente conhecida como produto de potências de bases iguais.
Devemos relembrar que produto é o resultado de uma multiplicação.
Então o produto de potências de bases iguais corresponde a multiplicação de números em forma de potência, cujas bases são idênticas.
Acompanhe os exemplos a seguir:
22 . 23
Note que temos duas potências sendo multiplicadas.
Antes de demonstrarmos a propriedade, vamos fazer os cálculos transformando as potências em seus respectivos resultados.
22 = 2 . 2
23 = 2 . 2 . 2
Assim, 22 . 23 = 2 . 2 . 2 . 2 . 2.
Isto significa que, após a multiplicação, a base 2 apareceu cinco vezes. Portanto, podemos representar o produto também em forma de potência: 25.
Olhe atentamente e perceba que a base 2 permaneceu inalterada. Observe ainda que os expoentes das potências anteriormente multiplicadas foram somados. Tínhamos os expoentes 2 e 3, sendo gerado o expoente 5. Confira mais uma vez:
22 . 23 = 25.
Diante do exposto, a presente propriedade nos garante que, para calcularmos o produto de potências com bases iguais, devemos conservar a base e somar os expoentes.
Assim:
22 . 23 = 2(2 + 3) = 25
Essa propriedade nos ajuda enormemente a calcular números grandes, conforme os exemplos seguintes.
56 . 57 = 2(6 +7) = 213
125 . 123 = 12(5 + 3) = 128
0,32 . 0,34 = 0,3(2 + 4) = 0,36
3-2 . 3-3 = 3-2 + (-3) = 3-2 - 3 = 3-5
x2 . x3 = x(2 +3) = x5
Divisão de potências de bases iguais
Em sentido oposto, quando ocorre a divisão de potências de mesma base, basta mantermos a base e subtrairmos os expoentes. É muito simples e fácil!
Vejamos alguns exemplos:
53 : 52 = 5(3 - 2) = 51 = 5
3-2 : 3-3 = 3-2 - (-3) = 3-2 + 3 = 31 = 3
y2 : y3 = y(2 - 3) = y-1
Potência de potência
Aprenderemos agora a propriedade popularmente conhecida como potência de potência.
Para representamos, veja o número abaixo:
(23)2
Veja que temos inicialmente o número 2 elevado a 3 entre parênteses.
Todo o número (base dois e expoente três) também está elevado a potência 2.
Realizando a fatoração, ou seja, representando as multiplicações, ficará assim:
(2 . 2 . 2)2
Ora, se o número 2 . 2. 2 está elevado ao quadrado (elevado à segunda potência), basta multiplicá-lo por ele mesmo:
(2 . 2 . 2) . (2 . 2 . 2)
Tirando os parênteses, obteremos o seguinte resutado:
2 . 2 . 2 . 2 . 2 . 2
A base 2 está sendo multiplicada 6 vezes. Isto significa que teremos 2 elevado a 6:
26
Então, já temos o resultado da nossa propriedade potência de potência:
(23)2 = 26
Repare nos expoentes das potências e irá constatar que ocorreu uma multiplicação entre eles: 3 x 2 = 6.
Isso comprova a propriedade da potência de potência, segundo a qual devemos manter a base e multiplicar os expoentes.
Retomando o exemplo, deve-se calcular assim:
(23)2 = 23 x 2 = 26
Acompanhe mais exemplos para aprender essa propriedade mais facilmente:
2 elevado a 5 elevado a 3
(25)3 = 25 x 3 = 215
3 elevado a 2 elevado a 4
(32)4 = 32 x 4 = 38
x elevado a 5 elevado a -3
(x5) -3= x5 x (-3) = x-15
👀 Cuidado com as casquinhas de banana!
Perceba que as potências de potências trazem consigo os parênteses.
Caso os parênteses não estejam presentes, o resultado será distinto. Iremos comprovar isso com um exemplo bem simples:
(23)4 = 23 x 4 = 212
Contudo, o número à esquerda é bem diferente. Neste caso, temos a base 2 elevada ao expoente 3, o qual está elevado a 4.
A solução requer primeiro a realização do cálculo da potência 3 elevado a 4, cujo resultado é 81.
Desta forma, o resultado é 281, totalmente diferente do anterior.
Potência de um produto
Produto nada mais é do que o resultado de uma operação de multiplicação. Olhe o seguinte exemplo...
(25 . 57)2
Veja que temos dois números em forma de potência sendo multiplicados e ambos estão elevados ao quadrado, pois eles estão entre parênteses.
Isso quer dizer que podemos reescrever os cálculos desta maneira:
(25 . 57) . (25 . 57) =
25 . 57 . 25 . 57 =
25 . 25 . 57 . 57 =
210 . 514
Retomando, então:
(25 . 57)2 = 210 . 514
Podemos concluir que, na potenciação de um produto, nós utilizamos a propriedade distributiva (apelidada de chuveirinho), segundo a qual o expoente que está fora dos parênteses deve multiplicar todos os expoentes no interior dos parênteses.
Veja que o expoente 2 multiplicou os expoentes 5 e 7, motivo pelo qual a base 2 passou a ter expoente 10 (2 x 5) e a base 5 passou a ter expoente 14 (2 × 7).
A mesma regra se aplica à potenciação de um quociente ou de uma divisão, onde o expoente que está fora dos parênteses deve multiplicar os expoentes do numerador e do denominador de uma fração.
Veja mais detalhes no próximo tópico.
Potenciação de fração
Até aqui, vimos potenciação com bases e expoentes constituídos de números inteiros. Porém, podem aparecer também números fracionários elevados a determinada potência, potência com expoentes fracionários.
Observe os exemplos e acompanhe as explicações.
Quando temos uma base fracionária entre parênteses significa que toda a fração está submetida ao expoente.
No exemplo acima você pode constatar que o expoente é aplicado ao numerador 1 e ao denominador 2.
Mas tenha bastante cuidado, pois se não houver o emprego dos parênteses o resultado será diferente. Acompanhe:
Nota-se claramente que o resultado mudou significativamente, haja vista que o expoente 3 foi aplicado apenas ao numerador da fração, mantendo-se o denominador inalterado.Potenciação com expoente negativo
As propriedades da potenciação com expoente negativo e fração com expoente negativo são praticamente idênticas.
Antes de estabelecermos o conceito, veremos como chegamos até ele.
Observe a seguinte sequência decrescente:
22 = 4
21 = 2
20 = 1
2-1 = 1/2
2-2 = 1/4
A sequência em questão é uma progressão geométrica de razão 1/2 (um meio).
Para saber várias coisas legais sobre esse assunto, acesse:
Perceba que, à medida em que o expoente decresce uma unidade, o resultado da potência decresce a metade.
Olhando para os dois últimos números (de cima para baixo), iremos constatar que eles são casos de potenciação com expoente negativo.
Também chegamos à constatação de que a potência com expoente negativo é inversa à mesma potência com valor positivo. Veja a ilustração:
O inverso de 2 é 1/2 (um meio) e o inverso de 4 é 1/4 (um quarto).
Vejamos esta propriedade em conjunto com a propriedade logo abaixo, a fim de extrairmos uma conclusão.
Fração com expoente negativo
Esta propriedade é uma coirmã da propriedade anterior!
Quando estivermos diante de uma fração com expoente negativo, devemos sempre invertê-la e trocar o sinal do expoente. Ou seja, o que é numerador vira denominador e o que é denominador vira numerador.
Assim, teremos uma fração invertida com o expoente positivo.
Acompanhe a gravura:
Potência com base 10
Veja algumas potências de base 10 e irá constatar uma propriedade interessante.
101 = 10
102 = 10 . 10 = 100
103 = 10 . 10 . 10 = 1000
Observe que o valor do expoente da potência de base dez corresponde exatamente ao total de zeros à direita do resultado.
Conclusão: em uma potência de base 10, o valor do expoente determina a quantidade de zeros à direita do algarismo após o resultado da potência.
Potência com base negativa
Quando estamos diante de uma potência com base negativa, devemos ficar muito atentos ao expoente, pois além de modificar o resultado da operação, o resultado poderá ser positivo ou negativo.
(-3)2 = (-3) . (-3) = 9.
De acordo com as regras da multiplicação, menos vezes menos é igual a mais, ou seja, a multiplicação de dois números negativos resultará inevitavelmente em um número positivo.
Vejamos agora outro exemplo:
(-3)3 = (-3) . (-3) . (-3) = -27.
Certamente, agora podemos perceber que além do valor da potência, o sinal agora ficou negativo. Isso porque multiplicamos menos vezes menos vezes menos, que é igual a menos.
(-) . (-) . (-) = -.
Após esses exemplos, já somos capazes de saber que em potência com base negativa, sempre que o expoente for par, o resultado será positivo.
Por outro lado, sempre que o expoente for ímpar, o resultado será negativo.
Conforme já alertamos, você deve ainda tomar muito cuidado com os parênteses na potenciação. Se determinado número negativo estiver funcionando como base, a correta análise e o uso dos parênteses será fundamental para que erros de cálculos sejam evitados.
Preste atenção aos exemplos adiante para ficar memorizar essa dica:
(3)2 = (-3) . (-3) = 9
Agora iremos retirar os parênteses...
- 32 = - 3 . 3 = - 9
Com a remoção dos parênteses, apenas o número 3 foi multiplicado por ele próprio. O sinal negativo foi conservado, pois ele não foi elevado ao quadrado.
Assim, o resultado da potência ficou negativo, diferentemente do obtido no exemplo anterior (positivo).
Potência com expoente fracionário
Entre os vários exemplos de potenciação, podemos observar um número elevado a fração.
Isso significa que podemos observar uma potenciação em que o expoente será fracionário.
Quando depararmos com um problema dessa natureza, devemos reescrever a potência, convertendo-a na operação denominada radiciação.
Em outras palavras, teremos que inserir o número descrito na base da potência em uma raiz.
O denominador da fração será deslocado para o grau da raiz.
Veja como é simples:
Todo número elevado a zero é igual a 1
Vamos agora comprovar mais uma das propriedades da potenciação. Observe a representação a seguir:
Para atribuirmos um significado a x0, isso dever ser feito de modo a continuar valendo a lei fundamental:
x a + b
Conforme uma propriedade estudada nesta aula textual, quando temos o produto de duas potências de mesma base, conservamos a base e somamos os expoentes.
Pois bem, iremos percorrer o caminho inverso agora, partindo da soma dos expoentes para o produto das potências:
x a + b = x a . x b
Agora vamos admitir que a é igual a zero (a = 0) e prosseguir calculando.
x 0 + b = x 0 . x b
Considerando ainda que x e b são valores não nulos, podemos simplificar os cálculos
x b = x 0 . x b
x b / x b = x 0
1 = x 0
Concluímos que x0 = 1.
Portanto, acabamos de comprovar mais uma das propriedades da potenciação, qual seja, todo número não nulo elevado a 0 é igual a 1.
Na potenciação sempre que a base for 1 a potência será igual a 1
Essa propriedade decorre da propriedade do elemento neutro da multiplicação.
O elemento neutro é exatamente o número 1.
Nesse sentido, qualquer número conserva o seu valor quando multiplicado por 1.
No caso da potenciação sempre que a base for 1 a potência será igual a 1.
Isso ocorre porque independentemente do valor do expoente o número 1 será sempre multiplicado por ele mesmo, mantendo o seu valor constante.
Por exemplo: 1 elevado a 1000 é igual a 1, visto que o 1 será multiplicado por ele mesmo mil vezes.
Exercícios de potenciação
Depois de uma longa jornada teórica, chegou um dos momentos que mais apreciamos: a resolução de exercícios.
Sempre procuramos disponibilizar questões de concursos públicos comentadas e com gabarito oficial.
Também buscamos abordar exercícios referentes a questões que foram alvo do Exame Nacional do Ensino Médio (Enem).
Exercício de potência #01
(VUNESP - 2021 - Semae de Piracicaba - SP - Assessor Administrativo - Encarregado de Serviço) Ao modelar uma situação, Vanessa precisou calcular o valor da potência 43/2 . Sabendo-se que o valor da potência foi calculado corretamente, ela encontrou, como resultado, o valor
a) 4.
b) 5.
c) 6.
d) 7.
e) 8.
Gabarito comentado!
Devemos relembrar a propriedade de potência com expoente fracionário, que envolve conhecimento mínimo de radiciação.
O denominador da potência fracionária converte-se no grau da raiz, assim:
43/2 = √43
Temos portanto uma raiz quadrada de 4 elevado a 3. Agora basta calcular:
√43 =
√64 =
8
Concluímos que o gabarito é a letra e.
Exercício de potência #02
(IBAM - 2020 - Prefeitura de Santos - SP - Oficial de Administração) Um piscicultor acaba de disponibilizar para venda sua produção de Tilápias que totaliza 8,34 toneladas. Sabendo que o peso médio de cada peixe para o abate é de 600 gramas, quantas unidades deste tipo de peixe, aproximadamente, serão disponibilizadas para comercialização por este produtor?
Alternativas
a) 1,38 . 103
b) 1,39 . 104
c) 1,38 . 105
d) 1,39 . 106
Comentários com gabarito!
Inicialmente, observe que o piscicultor disponibilizou o total de 8,34 toneladas de Tilápias para venda, sendo que cada peixe pesa 600 gramas.
A primeira coisa a se fazer nesta questão de potência é descobrir quantos gramas correspondem a 8,34 toneladas.
Primeiro, vamos converter toneladas para quilograma. Uma tonelada equivale a mil quilos. Então:
8,34 toneladas x 1000 = 8.340 kg
Um quilograma equivale a 1000 gramas. Então, façamos a conversão de kg para g:
8.340 kg x 1000 = 8.340.000 g
Pronto! agora já sabemos que o piscicultor dispões de 8.340.000 gramas de peixe Tilápia para venda e cada um desses peixes possui 600 gramas de massa.
Para resolvermos definitivamente o exercício de potência é suficiente dividirmos 8.340.000 gramas por 600 gramas. Assim iremos descobrir quantos peixes o piscicultor possui.
8.340.000 : 600 = 13.900 peixes.
Também podemos elaborar uma regra de três simples para resolvermos a questão de potenciação em evidência:
1 peixe ⟶ 600g
x peixe ⟶ 8.340.000 g
Fazendo a multiplicação cruzada, teremos:
600g . x = 8.340.000 g
x = 8.340.000 g/600g
x = 13.900 peixes.
Temos o quantitativo total de peixes. O problema é que a questão pede o número em forma de potência, motivo pelo qual temos que realizar a conversão.
Trata-se de potência de base 10.
Para facilitar a resolução, consideremos de início que 13.900 equivale 139 . 100 (observe que 100 vezes 139 é igual a 13.900).
Transformando 100 em potência, temos 102.Vamos organizar os dados:
139 . 100 =
139 . 102 =
Observando os itens da questão, constata-se que há números 1,39. Então vamos adequar 139 para 1,39 e efetivar os cálculos finais:
(1,39 . 100) . 102 =
(1,39 . 102) . 102 =
1,39 . 102 . 102 =
1,39 . 104
Portanto, gabarito: letra c.
Exercício de potência #03
(Quadrix - 2021 - CRBio-6ª Região - Auxiliar de Serviços Gerais) João, um biólogo, utiliza um método matemático para estimar a velocidade de um peixe. A partir desse método, ele verificou que a velocidade do peixe era igual a (5121/3)3/2 quilômetros por hora.
Com base nesse caso hipotético, assinale a alternativa correta.
a) A velocidade do peixe, em quilômetros por hora, é representada por um número racional.
b) A velocidade do peixe, em quilômetros por hora, é representada pelo número dado por 16√2.
c) A velocidade do peixe, em quilômetros por hora, é representada por um número natural.
d) A velocidade do peixe, em quilômetros por hora, é representada pelo número dado por 16∛2.
e) A velocidade do peixe, em quilômetros por hora, é representada pelo número dado por 32√2.
Comentários com resposta e gabarito!
Para calcularmos a velocidade do peixe, devemos inicialmente desenvolver o número em forma de potência.
Devemos lançar mão de duas propriedades: potência de potência e potência com expoente fracionário. Mãos à obra!
(5121/3)3/2
Antes de tudo, como temos potência de potência, vamos multiplicar os expoentes:
O novo expoente é 1/2 (um meio). Então, temos:5121/2
O número que expressa a razão existente entre o comprimento do diâmetro de um fio de cabelo e o de um nanofio é
Agora, o próximo passo é fatorar o número 512. A fatoração de um número inteiro nada mais é do que a sua transformação de um número inteiro em números menores multiplicados. Por exemplo: o número 12 fatorado é 2 . 2 . 3.
Para fatorarmos um número, devemos efetivar várias operações de divisão!
Passemos então à fatoração do número 512:
Perceba que foi bastante simples. Os números da esquerda foram sucessivamente divididos pelos números da direita.
Agora veja que à direita o número 2 apareceu 9 vezes. Isso significa que a fatoração é 2 x 9? A resposta é não! Muita calma nessa hora!
Se o número 2 apareceu 9 vezes, então temos aqui uma operação de potenciação, ou seja, temos 2 elevado a nona potência. Assim:
👉 29
Então vamos reescrever o número 512 já fatorado:
5121/2
(29 )1/2
Lembre-se de da propriedade do produto de potências de mesma base. Conservamos a base e somamos os expoentes. Assim 29 pode ser escrito como 2. 28. Continuando...
(2. 28 )1/2
Usando a propriedade distributiva (chuveirinho):
21/2. 28 . 1/2
21/2. 24
21/2. 16
16 . 21/2
Agora, para finalizar, usaremos novamente mais uma propriedade: potência com expoente fracionário!
Veja que o número 2 está elevado a 1/2 (um meio). O denominador do expoente fracionário é justamente 2.
Desta forma, devemos transformar a potência de base 2 em uma raiz quadrada.
21/2 = √2
Por fim, temos que...
16 . 21/2
16 . √2
Portanto, o gabarito da nossa questão é a letra b.
Notou a importância de se resolver muitos exercícios de potenciação? Veja que em apenas uma questão tivemos que aplicar conhecimentos envolvendo várias propriedades da potenciação.
Exercício de potenciação #04
(Quadrix - 2021 - CRTR - 12ª Região - Agente Fiscal) Assinale a alternativa que apresenta a quantidade de segundos que tem um ano bissexto (366 dias).
a) 28 . 34 . 52 . 61
b) 28 . 32 . 54 . 61
c) 28 . 33 . 53 . 61
d) 26 . 33 . 5 . 61
e) 26 . 33 . 5 . 61
Essa questão de potenciação é muito interessante porque aborda um tema de conhecimento prático do nosso quotidiano. Vamos calcular a quantidade de segundos correspondente a um ano bissexto, ou seja, um ano de 366.
Se você não sabe o que é um ano bissexto, nós ensinamos isso em um de nossos artigos. Dá uma conferida lá para aprender isso de uma maneira muito fácil:
Retomando a nossa questão, vamos converter ano em segundos através de etapas:
1 ano bissexto tem 366 dias
1 dia tem 24 horas
1 hora tem 60 minutos
1 minuto tem 60 segundos
Para que a transformação de medias de tempo aconteça, devemos multiplicar tudo:
366 . 24 . 60 . 60
Se você olhar novamente as alternativas apresentadas na questão, irá perceber que os números estão escritos em forma de potência. Então devemos fatorar os números para chegarmos à resposta correta (reveja a explicação sobre fatoração da questão antecedente).
366 . 24 . 60 . 60
(2 . 3 . 61) . (2 . 2 . 2 . 3) . (2 . 2 .3 . 5) . (2 . 2 .3 . 5)
Pronto, já temos os números fatorados. Agora devemos transformá-los em potências...
(2 . 3 . 61) . (23 . 3) . (22 .3 . 5) . (22 .3 . 5)
Retirando os parênteses...
2 . 3 . 61 . 23 . 3 . 22 . 3 . 5 . 22 . 3 . 5
Para ficar mais organizado, vamos aproximar as potências de mesma base...
2 . 23 . 22 . 22 . 3 . 3 . 3 . 3 . 5 . 5 . 61
Para finalizarmos o exercício de potenciação, devemos somar os expoentes cujas bases seja iguais, conservando a base...
2(1 + 3 + 2 + 2) . 3(1 + 1 + 1 + 1) . 52 . 61
28 . 34 . 52 . 61
Logo, o gabarito da questão é a letra a.
Exercício de potenciação #05
(INEP - 2021 - ENEM - Exame Nacional do Ensino Médio - Primeiro e Segundo Dia - PPL) Se a tartaruga, a lesma e o caramujo apostassem uma corrida, a lesma chegaria em último lugar, o penúltimo colocado seria o caramujo e a primeira seria a tartaruga. Segundo o biólogo americano Branley Allan Branson, a velocidade “recorde” já registrada em pesquisas, por uma lesma, é de 16,5 centímetros por minuto.
Disponível em: (sítio eletrênico mundo estranho). Acesso em: 6 jul. 2015.
Para uma reportagem, dispondo das velocidades recordes da tartaruga e do caramujo em metro por segundo, se faz necessário saber o fator de conversão da velocidade recorde da lesma para metro por segundo para divulgar uma comparação.
Com base nas informações, o fator de conversão da velocidade recorde da lesma para metro por segundo é
a) 10-2 × 60-2
b) 10-2 × 60-1
c) 10-2 × 60
d) 10-3 × 60-1
e) 10-3 × 60
Gabarito comentado!
A questão traz um blá blá blá interessante sobre a velocidade de animais extremamente lentos por natureza ("véi" quem perde tempo calculando velocidade de tartarugas, lesmas e caramujos? 😂).
O cerne da questão paira sobre a velocidade recorde da lesma: incríveis 16,5 centímetros por minuto.
Depois de toda a historinha típica das provas do Enem, a questão requer o fator de conversão da velocidade recorde da lesma para metro por segundo.
Então temos uma velocidade em centímetros por minuto que deve ser convertida para metros por segundo:
cm/min ➡ m/s
Detalhando, temos que converter cm para m e min para s.
cm para m
1 metro equivale a 100 centímetros. Em sentido inverso, 1 centímetro equivale a 0,01 m. Nós explicamos isso detalhadamente no artigo: 1 metro tem quantos centímetros.
Como já sabemos, 100 pode ser escrito em forma de potência de base 10. Assim:
100 = 102.
Como estamos convertendo de centímetro para metro, isto é, de uma medida menor para uma menor, devemos efetuar a divisão por 100, resultando em 0,01.
0,01 = 1/100
1/100 = 10-2
Portanto, o fator de conversão de medidas é 10-2.
min para s
Para convertermos minutos para segundo é muito simples: 1 minuto equivale a 60 segundos.
Mas não se esqueça de que velocidade é espaço sobre tempo. Assim, o tempo fica no denominador da fração, motivo pelo qual usamos o expoente negativo.
Assim, o fator de conversão de tempo é 60-1.
Logo, o fator de conversão da velocidade da lesma é:
10-2 × 60-1
Isso nos leva à conclusão de que o gabarito é a letra b.
Exercício de potenciação #06
(INEP - 2021 - ENEM - Exame Nacional do Ensino Médio - Primeiro e Segundo Dia - PPL) O nanofio é um feixe de metais semicondutores usualmente utilizado na fabricação de fibra óptica. A imagem ilustra, sem escala, as representações das medidas dos diâmetros de um nanofio e de um fio de cabelo, possibilitando comparar suas espessuras e constatar o avanço das novas tecnologias.
a) 6 × 10-14
b) 6 × 10-5/9
c) 6 × 105/9
d) 6 × 104
e) 6 × 1045
Comentários com gabarito!
A razão entre dois números nada mais é do que o quociente da divisão entre eles.
Dessa forma, a razão entre o comprimento do diâmetro de um fio de cabelo e o de um nanofio é a divisão entre as respectivas medidas, ou seja:
Diâmetro do fio de cabelo/Diâmetro do nanofio
6 × 10-5/10-9
Acompanhe o cálculo com a potência de base 10:
Exercício de potenciação #07
(INEP - 2015 - ENEM - Exame Nacional do Ensino Médio - Primeiro e Segundo Dia) As exportações de soja do Brasil totalizaram 4,129 milhões de toneladas no mês de julho de 2012, e registraram um aumento em relação ao mês de julho de 2011, embora tenha havido uma baixa em relação ao mês de maio de 2012.
Disponível em: www.noticiasagricolas.com.br. Acesso em: 2 ago. 2012.
A quantidade, em quilogramas, de soja exportada pelo Brasil no mês de julho de 2012 foi de
a) 4,129 X 103
b) 4,129 X 106
c) 4,129 X 109
d) 4,129 X 1012
e) 4,129 X 1015
Comentários!
Fechando com chave de ouro, vamos resolver uma questão de potenciação que abrange a propriedade de potência de base dez.
O enunciado aponta um número em toneladas e requer o respectivo valor em quilogramas.
Exportação: 4,129 milhões de toneladas.
Ou seja:
4,129 x 1.000.000 =
Em vez de multiplicar diretamente, é mais útil representarmos o milhão em forma de potência: 106
4,129 x 106 toneladas
👉 1 tonelada = 1.000 quilogramas.
Agora basta converter toneladas para quilogramas, multiplicando o valor por mil:
Assim:
4,129 x 106 x 1000 =
Escrevendo 1000 em potência, obteremos 103:
4,129 x 106 x 103 =
4,129 x 109
Portanto, o nosso gabarito é a letra c.
Finalmente, encerramos o nosso assunto potenciação: propriedades, exercícios e exemplos. Procuramos desenvolver o conteúdo mais completo possível, pois se trata de um assunto de extrema relevância para todos nós.
Também é constantemente cobrado em provas de concursos, vestibulares e do Enem.
Esperamos que esta aula textual tenha te ajudado a aprender um pouco mais sobre matemática.
Bons estudos e até a próxima!
Tags
Matemática