Nesta exposição matemática, vamos explicar o que são ângulos opostos pelo vértice, assim como veremos exemplos e exercícios para ilustrar e facilitar a assimilação do conteúdo a ser estudado.
Observe apenas a reta a e perceba que ela separa os ângulos x (em verde) e z (na cor laranja). Note que o ângulo verde (x) está na parte superior da reta. Já o ângulo laranja (z) se encontra na parte inferior.
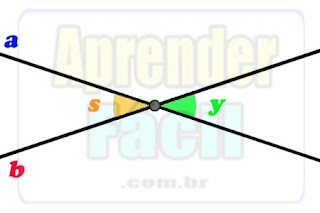
Novamente temos as retas a e b separando ângulos em lados opostos. Neste caso, a reta a estabelece que o ângulo y fica em sua parte superior e o ângulo s na parte inferior.
Apenas com esses dois conceitos básicos, é possível resolvermos muitos exercícios envolvendo problemas com ângulos. Confira a seguir.
Desde já, destacamos que existem vários tipos de ângulos, entre eles: reto, agudo, obtido, complementares etc.
Se você quer saber mais sobre os ângulos, clique e acesse o conteúdo a que preparamos detalhadamente:
Também não deixe de tentar responder ao seguinte desafio:
Ângulos opostos pelos vértice
A nomenclatura nos ajuda bastante a entender o que são ângulos opostos pelo vértice.
Inicialmente, trata-se exatamente de ângulos que se encontram em lados ou posições opostas.
E o que está entre eles? Como não poderia deixar de ser, é exatamente o vértice dos ângulos.
Vamos explicar tudo detalhadamente abaixo.
O que é vértice
Antes de tudo, devemos entender que um ângulo é a abertura entre duas semirretas.
Por sua vez, semirreta é a parte de uma reta que possui apenas um início, ou seja, a semirreta se inicia em seu ponto de origem e passa por infinitos pontos, significando assim que ela possui início mas não tem fim.
Para facilitar o entendimento, visualize em sua mente os ponteiros de um relógio. Eles são como semirretas.
Dessa maneira, é exatamente na origem da semirreta que se encontra o seu vértice.
Na verdade, o vértice é o encontro de duas ou mais semirretas, que juntas formam o ângulo. Ainda imaginando o relógio, o vértice é o ponto de origem dos ponteiros.
Sabendo disso, agora poderemos avançar no entendimento do conteúdo.
Retas concorrentes
Duas retas podem se posicionar de forma paralela, ou seja, possuindo exatamente a mesma inclinação e nunca se cruzando.
No entanto, as retas podem se cruzar em apenas um ponto. Neste caso, nós dizemos que as retas são concorrentes.
Quando duas retas concorrentes se cruzam, elas formam quatro ângulos. Além disso, as duas retas constituem quatro semirretas, cuja origem em comum é o vértice dos ângulos formados pelo cruzamento.
O que são ângulos opostos
Conforme já explicamos acima, os ângulos opostos, como o próprio nome já nos diz, são angulações que estão em posições opostas. Isso é meio obvio, mas como podemos identificar os lados opostos?
É muito simples, basta que prestemos atenção aos lados estabelecidos pelas retas.
Vejamos a seguinte imagem:
Observe apenas a reta a e perceba que ela separa os ângulos x (em verde) e z (na cor laranja). Note que o ângulo verde (x) está na parte superior da reta. Já o ângulo laranja (z) se encontra na parte inferior.
Portanto, significa que a reta a separa os ângulos x e z em lados opostos.
Da mesma forma, a reta b separa os referidos ângulos, deixando-se em lados opostos.
Quando os ângulos se opõem simultaneamente (ao mesmo tempo) em relação às duas retas, obrigatoriamente esses ângulos também serão opostos em relação ao vértice, que conforme já explicamos é o ponto de encontro entre as retas envolvidas no exemplo citado.
O fenômeno ocorre de forma semelhante com os demais ângulos decorrentes do cruzamento das retas, como podemos constatar na imagem logo abaixo:
Novamente temos as retas a e b separando ângulos em lados opostos. Neste caso, a reta a estabelece que o ângulo y fica em sua parte superior e o ângulo s na parte inferior.
Por sua vez, a reta b posiciona o ângulo s no lado superior e o ângulo y no lado inferior.
Como os ângulos s e y se posicionam simultaneamente em lados opostos em relação às duas retas, esses ângulos também são opostos em relação ao vértice.
Podemos adotar outro raciocínio para ajudar na definição do que são ângulos opostos pelo vértice.
Conforme já explicitado, quando duas retas se encontram, formam-se quatro semirretas com um vértice em comum.
Diante disso, podemos concluir facilmente que cada reta forma duas semirretas que se tornam opostas em relação ao vértice.
Assim, como os ângulos são formados a partir da abertura entre as semirretas, podemos chegar à conclusão de que os ângulos também serão opostos pelo vértice.
Ângulos opostos pelo vértice são congruentes
Depois de analisados os conceitos que cercam o tema proposto, veremos agora algumas propriedades muito importantes sobre ele.
A primeira é que quando dois ângulos estão opostos pelo vértice, nos termos descritos acima, podemos assegurar tranquilamente uma coisa: eles são congruentes!
Como sinônimos da palavra congruente, temos: coincidente ou correspondente em características, em propriedades; conforme, concordante, harmônico.
Isto significa matematicamente que os ângulos opostos pelo vértice possuem exatamente a mesma medida.
No exemplo visto na primeira imagem, se o ângulo x medir 120º (cento e vinte graus), podemos afirmar com segurança que o ângulo z também mede 120º, pois eles são congruentes.
👉 Matematicamente, temos que:
x = z
s = y
Ângulos adjacentes são suplementares
Você já sabe que, após o encontro de duas retas, os ângulos opostos pelo vértice são congruentes.
No entanto, outra propriedade importante nos informa que os ângulos adjacentes são suplementares.
Em outras palavras, os ângulos que estão dispostos lado a lado equivalem a um ângulo raso, medindo exatamente 180º (cento e oitenta graus).
Observe a ilustração:
Preste bastante atenção à imagem acima e note que os ângulos y e z estão situados um ao lado do outro, motivo pelo qual são classificados como adjacentes.
Também podemos notar que os referidos ângulos estão delimitados exatamente sobre a reta a, formando um ângulo raso, ou seja, de 180º (cento e oitenta graus). Por isso, os referidos ângulos são classificados como suplementares.
👉 Matematicamente, temos a seguinte fórmula:
y + z = 180º.
Ângulos opostos pelo vértice exercícios
Chegou a hora de praticar! Veremos alguns exercícios a fim de fixarmos a teoria que envolve o assunto em foco.
Exercício #01
Analisando-se os ângulos a seguir, calcule e descubra os valores de x, y e z.
O primeiro passo para a resolução do exercício é estabelecermos o valor de x, pois ele está em local oposto ao ângulo de 60º (sessenta graus).
Lembra que os ângulos opostos pelo vértice são congruentes? Pois bem, se eles são congruentes, então eles possuem exatamente a mesma medida.
Diante dessa informação, já podemos concluir que o valor de x também mede 60º.
👉 x = 60º.
Agora vamos descobrir as medidas dos ângulos restantes.
O próximo raciocínio é o seguinte: ângulos adjacentes são suplementares, ou seja, a soma de suas medidas corresponde a 180º (cento e oitenta graus).
Então vamos fazer a seguinte equação:
60º + y = 180º
y = 180º - 60º
y = 120º
Observe que os ângulos y e z (na cor azul) também são opostos pelo vértice. Sendo assim, eles possuem a mesma medida.
Como já descobrimos que y mede 120º, então a medida de z é exatamente 120º.
Finalmente já sabemos os valores dos ângulos x, y e z:
👉 x = 60º.
👉 y = 120º.
👉 z = 120º.
Exercício #02
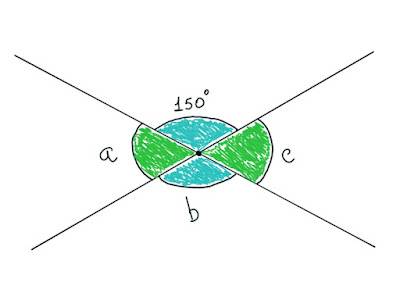
Considerando os ângulos opostos pelo vértice abaixo, calcule os valores de a, b e c.
Vamos resolver a questão usando um raciocínio um pouco diferente. Mas o raciocínio do exercício anterior também é suficiente para chegarmos à resposta correta.
Observe a imagem e perceba que a soma de todos os quatro ângulos correspondem a uma volta completa. Significa dizer que a soma dos todos os ângulos corresponde a 360º.
Vamos organizar tudo matematicamente:
a + b + c + 150º = 360º
Já sabemos que o ângulo b é oposto pelo vértice em relação ao ângulo de 150º.
Assim, b também mede 150º, pois ambos são congruentes.
Continuando a resolução do exercício, vamos substituir o valor de b na equação:
a + 150º + c + 150º = 360º
Agora observe que a e c também são ângulos opostos pelo vértice. Então podemos seguramente chamar c de a. fica assim:
a + 150º + a +150º = 360º
2a + 150 + 150º = 360º
2a + 300º = 360º
2a = 360º - 300º
2a = 60º
a = 60º / 2
a = 30º
Portanto:
👉 a = 30º.
👉 b = 150º.
👉 c = 30º.
Exercício #03
Com base nos ângulos opostos pelo vértice, calcule o valor de x.
O raciocínio é perfeitamente o mesmo: ângulos opostos pelo vértice são congruentes.
Assim, podemos organizar uma equação correspondente aos ângulos em azul, visto que ambos possuem exatamente a mesma medida. Matematicamente:
7x + 50 = x + 110
Agora, temos uma equação de primeiro grau bastante simples. Continuemos a solução...
7x - x = 110 - 50
6x = 60
x = 60/6
x = 10.
Pronto, x é igual a 10.
Substituindo o valor de x por 10, seremos capazes de descobrir os valores dos ângulos correspondentes. Veja:
7x + 50
7*10 + 50
70 + 50
120º
Assim, os ângulos opostos medem 120º e 60º.
Essas foram as principais informações sobre o tema ângulos opostos pelo vértice. Vimos teoria, exemplos e exercícios resolvidos. Caso tenha ficado alguma dúvida, poste-a nos comentários. Bons estudos!
Tags
Matemática