Os ângulos são quase imperceptíveis no nosso quotidiano, mas eles estão em toda parte! Para comprovar isso, basta imaginarmos por exemplo que os ponteiros do relógio formam ângulos entre si, bem como as paredes de uma casa também constituem um ângulo reto em relação ao solo.
Dica de memorização: associe a palavra obtuso à palavra obturação. Sim, aquele procedimento dentário em que nós temos que abrir bem a boca. É estranho mas funciona de verdade!
Podemos enxergar claramente que as semirretas OA e OB formam um ângulo nulo entre si, ou seja, um ângulo de 0º.
Existem inúmeros exemplos de ângulos nulos no nosso dia a dia. Basta imaginarmos uma porta completamente fechada, assim como um caderno perfeitamente fechado, para termos uma ideia do que é um ângulo nulo.
Vamos por partes!
Como podemos ver, os ângulos alfa e beta estão em lados opostos também em relação às retas que os formaram.
De acordo com a ilustração, a soma do ângulo A, em azul, com o ângulo B, em vermelho, é igual a 90º.
Seguindo-se os mesmos passos para o entendimento dos conceitos observados acima, a soma dos ângulos D e A é igual a 360 graus (360º).
Na ortopedia, que é uma área da medicina, os ângulos são usados para identificar o grau de uma doença da coluna denominada escoliose.
Outrossim (igualmente), na engenharia de tráfego, os ângulos são amplamente utilizados para medição da inclinação de ruas e estradas.
Além de tudo isso, eles estão muito presentes no estudo teórico da geometria e da trigonometria, que por sua vez fazem parte da matemática.
Assim percebe-se que os ângulos podem ser, entre outros: retos, agudos, obtusos, e rasos. Fique bem tranquilo, pois são muitos conceitos de simples compreensão.
Podemos identificar facilmente o ângulo reto por meio de sua representação: um quadradinho e uma bolinha em seu interior.
Neste caso, digamos que as semirretas são a parede que está sendo construída e o solo (chão).
Diante da enorme importância dos ângulos, vamos explicar nesta oportunidade o que é um ângulo agudo, assim como o que são ângulos: obtuso, reto, raso e nulo. E ainda vamos detalhar as relações entre as angulações para que você saiba praticamente tudo sobre o conteúdo.
Importante: esta postagem se encontra recheada de imagens, a fim de tornar o conteúdo bastante claro e fácil de se entender.
Sempre que quiser retomar algum tema específico, basta navegar pelo nosso índice:
{getToc} $title={Índice da aula textual}
Vamos aos conceitos e exemplos!
O que é um ângulo
O conceito de ângulo é bem simples: trata-se de um ponto ou abertura que se forma onde duas semirretas se encontram.
Mas o que são semirretas? Você poderia estar se perguntando agora.
Semirretas são as partes de uma reta que se originam em um ponto mas que não têm fim.
Por exemplo: a semirreta AB→ se inicia no ponto A, passa pelo ponto B e segue infinitamente, ou seja, por infinitos pontos.
O ponto de encontro entre duas semirretas é chamado de vértice do ângulo. Essa informação é relevante, pois os vértices estão muito presentes no estudo da geometria plana.
Conforme já explicado no início, existem vários tipos de ângulos, cujas medidas são realizadas através do grau, que é representado pelo símbolo: ° (uma bolinha sobrescrita).
O grau é uma medida de ângulos planos, o qual corresponde a 1/360 de uma circunferência, ou seja, uma parte do todo, que mede 360º.
Importante destacarmos também que cada grau pode ser dividido em minutos (′), os quais equivalem a 1/60 do grau, e em segundos (′′), equivalendo a 1/60 do minuto.
Para medirmos os ângulos com exatidão em nossas atividades escolares ou até mesmo do dia a dia, devemos usar um instrumento denominado transferidor, o qual é um objeto em formato circular que pode ser encontrado nos modelos de 90°, 180° e 360°.
Assim como nas réguas, as quais são divididas em centímetros, os transferidores são divididos de grau em grau. Separamos imagens de transferidores no decorrer da apresentação.
Não perca essas dicas:
De acordo com Sistema Internacional de Unidades, os ângulos são mensurados através de uma unidade chamada de radiano (rad).
Exemplos de ângulos
Observe a imagem para visualizar facilmente o que é um ângulo.
Vejamos a seguir cada um deles.
O que é um ângulo reto
Iniciaremos pelo ângulo reto, pois ele é uma referência para o estudo do ângulo agudo e obtuso.
O ângulo reto é aquele que mede exatamente noventa graus, 90º, o que corresponde a um quarto (1/4) de uma volta.
Para ter uma ideia, imagine-se cortando uma pizza em quatro partes iguais. Cada uma dessas partes formaria um ângulo reto, ou seja, de 90º entre si.
Veja uma ilustração para facilitar o entendimento:
Esses importantes ângulos se caracterizam por apresentarem uma relação de perpendicularidade entre as duas semirretas que os formam.
Em outras palavras uma semirreta forma posição vertical em relação à outra, que está na horizontal.
Ângulo reto exemplos
Na construção civil, diz-se que algo está no esquadro ou no prumo exatamente quando as semirretas correspondentes formam um ângulo de noventa graus.
Veja esse exemplo:
Neste caso, digamos que as semirretas são a parede que está sendo construída e o solo (chão).
Para medir o ângulo formado entre o chão e a parede, o profissional usa o prumo, conforme se observa na imagem.
Assim, através da força da gravidade, o pêndulo fica na posição vertical indica se a parede também está alinhada exatamente na vertical em relação ao solo, formando com este o ângulo de 90º.
O esquadro é mais empregado para se medir ângulos retos formados entre paredes, terrenos, móveis etc.
Apenas para complementar: na trigonometria, existe o triângulo retângulo, o qual se caracteriza exatamente por causa da existência de um ângulo reto.
Em seu estudo, deve-se usar o conhecidíssimo Teorema de Pitágoras, que afirma que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
Mas não se apegue a esse conceito agora, pois vamos nos aprofundar no assunto apenas em outra ocasião.
O que é um ângulo agudo
Agora que já sabemos o que é um ângulo reto, fica mais fácil sabermos o que é um ângulo agudo e também o que é um ângulo obtuso, pois os ângulos retos são as nossas medidas de referência.
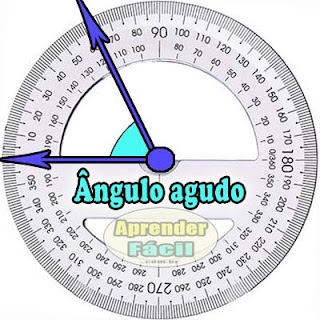
A definição ficou bastante simples: ângulo agudo é aquele cuja medida é maior que 0 grau e menor que 90 graus.
Em outras palavras, temos um ângulo agudo quando sua medida é maior que a de um ângulo nulo e menor do que a medida do ângulo reto.
Em uma representação matemática simples, temos que: 0º < ângulo agudo < 90º
Dica de memorização: associe a palavra agudo à palavra agulha, a fim de lembrar mais facilmente que o ângulo agudo é menor que o reto e o obtuso, pois uma agulha é bem pequena e nos ajuda a memorizar a informação.
Observe esta imagem de um ângulo agudo representada por meio de um transferidor:
Ângulo agudo exemplos
Um dos principais exemplos de ângulo agudo no nosso dia a dia é o das pinças. As hastes das pinças são como as semirretas que formam um ângulo menor que 90 graus. Veja:
O que é um ângulo obtuso
Ângulo obtuso é aquele cuja medida é maior que noventa graus e menor que cento e oitenta graus. Significa que ele é maior que o ângulo reto e menor que o ângulo raso.
Em uma linguagem matemática, podemos dizer que esse ângulo é maior que 90º e menor que 180º, ou ainda: 90º < ângulo obtuso < 180º.
Veja a indicação de um ângulo obtuso através de um transferidor:
Veja a indicação de um ângulo obtuso através de um transferidor:
Dica de memorização: associe a palavra obtuso à palavra obturação. Sim, aquele procedimento dentário em que nós temos que abrir bem a boca. É estranho mas funciona de verdade!
Imagine-se abrindo a boca em um ângulo maior que noventa graus e nunca mais esqueça o que é um ângulo obtuso 😁.
Ângulo obtuso exemplos
Um dos exemplos práticos mais comuns de ângulos obtusos vem da tecnologia. Trata-se de um dos aparelhos eletrônicos mais utilizados do mundo: o notebook.
Quem usa essa equipamento, sabe que ele deve ficar bem aberto para que as imagens possam ser bem observadas na tela.
Em outras palavras, para melhor experiência do usuário, a tela do notebook deve fazer um ângulo obtuso em relação à base do aparelho, onde se localiza o teclado. Veja a imagem ilustrativa:
O que é um ângulo raso
O conceito de ângulo raso é bem simplório: trata-se do ângulo cuja medida é exatamente 180 graus. Matematicamente: 180º.
Esse ângulo também é conhecido como meia-volta, haja vista que ele representa a metade de uma volta completa.
O ângulo raso se caracteriza ainda pelo fato de que as semirretas que o formam se alinham em sentidos opostos como se constituíssem apenas uma reta.
Veja um exemplo na imagem adiante:
Ângulo raso exemplos
O exemplo mais comum de ângulo raso para os estudantes é o caderno.
Quando um caderno está totalmente aberto sobre uma mesa plana, suas folhas são como semirretas que formam um ângulo raso entre si.
Confira a imagem ilustrativa:
O que é um ângulo nulo
A palavra nulo já denota a ideia de algo inexistente, nenhum etc. Nesse sentido, um ângulo nulo nada mais é do que um ângulo de zero grau (0º).
Cuidado para não confundir ângulo raso com ângulo nulo. O ângulo raso é formado por duas semirretas que se alinham em sentidos opostos.
Já o ângulo nulo é formado por duas semirretas que se alinham no mesmo sentido.
Veja a imagem:
Existem inúmeros exemplos de ângulos nulos no nosso dia a dia. Basta imaginarmos uma porta completamente fechada, assim como um caderno perfeitamente fechado, para termos uma ideia do que é um ângulo nulo.
Se visualizarmos também a posição dos ponteiros de um relógio exatamente ao meio dia, teremos a constatação de que os referidos ponteiros formam um ângulo nulo entre si.
Vimos, portanto, as principais definições acerca dos ângulos existentes.
A partir de agora, veremos a relação que existe entre os mais diversos ângulos entre si.
Ângulos consecutivos
Preste muita atenção para não confundir ângulos consecutivos com ângulos adjacentes, que veremos a seguir.
Ângulos consecutivos são aqueles que possuem pelo menos um lado e um vértice em comum.
Observe o raciocínio através da gravura a seguir:
Vamos por partes!
Primeiramente, devemos ligar os pontos referentes ao ângulo beta: XOY (ângulo menor).
Agora repare que se somarmos os ângulos azul e vermelho, teremos um novo ângulo, que é maior, formado pelos pontos XOZ, que corresponde exatamente a um ângulo reto, medindo 90º.
Preste bastante atenção que os ângulos XOY (menor) está contido no ângulo XOZ (maior) e eles possuem um lado em comum, no caso XO, e o vértice O.
Esse detalhe é fundamental: um ângulo está contido no outro ou mantém pontos em comum com ele.
Se dois ângulos estiverem lado a lado e não estiverem contidos um no outro ou não apresentarem pontos em comum, então eles serão consecutivos e também adjacentes, conforme a explicação imediatamente abaixo.
Ângulos adjacentes
A palavra adjacente significa posto ao lado de; junto, pegado; situado em local próximo, confinante, contíguo, vizinho.
Esse conceito se aplica matematicamente ao conceito de ângulos adjacentes, pois estes se encontram no mesmo lado do vértice.
Visualize:
Assim, os ângulos alfa e beta são adjacentes porque um não está contido no outro e não há pontos em comum entre eles.
O principal detalhe é que estão dispostos lado a lado.
Ângulos opostos pelo vértice
Esses ângulos são resultado do cruzamento de retas. Significa que, quando duas retas se cruzam, formam-se quatro semirretas.
Como o próprio nome sugere, os ângulos opostos pelo vértice encontram-se em posições opostas em relação ao vértice deles. O conceito é bem simples assim mesmo, conforme a ilustração geométrica:
Como podemos ver, os ângulos alfa e beta estão em lados opostos também em relação às retas que os formaram.
O que os separa é exatamente o vértice comum entre os ângulos.
Uma característica interessante dos ângulos opostos pelo vértice é que eles são congruentes. Isso significa que eles têm a mesma medida.
Ângulos complementares, suplementares e replementares
Nós vimos até aqui os diversos tipos de ângulos. Contudo, agora veremos conceitos relacionados a operações matemáticas simples entre os mais distintos ângulos existentes.
Ângulos complementares
O primeiro desses conceitos é o de ângulos complementares, que são aqueles cujas somas equivalem ao ângulo reto.
Em outras palavras, a soma de dois ou mais ângulos complementares é igual a 90 graus (90º).
Observe a imagem:
Assim, por exemplo, se você já souber que o ângulo A é de 40º, e quiser descobrir o valor de B, basta fazer uma continha simples: A + B = 90º ⇒ 40º + B = 90º ⇒ B = 90º - 40º.
👉 90 - 40º = 50º.
O complemento de um ângulo é o valor que falta para a soma completar o valor de 90º. Ou seja, o complemento de A é B e o complemento de B é A.
Isso é muito cobrado em vestibulares e muitas vezes em provas do Enem.
Ângulos suplementares
O conceito de ângulos suplementares é semelhante ao conceito de ângulos complementares.
A diferença é que a soma dos ângulos suplementares equivale a um ângulo raso, ou seja, será igual a 180 graus (180º).
Veja no desenho:
Usando o mesmo raciocínio do conceito imediatamente anterior, podemos perceber que a soma dos ângulos C e A é igual a 180º.
Da mesma forma, se já dispusermos do valor de um dos ângulos, podemos descobrir o valor do outro.
Por exemplo, se o ângulo A medir 30º, é suficiente fazermos uma conta básica para descobrirmos o valor de C:
👉 180º - 30º = 150º.
O suplemento de um ângulo é o valor que falta para a soma completar o valor de 180º. Ou seja, o suplemento de A é B e o suplemento de B é A.
Ângulos replementares
Por fim, temos os chamados ângulos replementares, cujas somas equivalem ao ângulo de 360º, que por sua vez corresponde a uma volta completa.
Mais uma ilustração para facilitar:
Seguindo-se os mesmos passos para o entendimento dos conceitos observados acima, a soma dos ângulos D e A é igual a 360 graus (360º).
Caso saibamos o valor de A, é possível descobrirmos o valor de D. Por exemplo, se A mede 20º, teremos de fazer o seguinte cálculo.
👉 360º - 20º = 340º.
O replemento de um ângulo é o valor que falta para a soma completar o valor de 360º. Ou seja, o replemento de A é B e o replemento de B é A.
Fácil, não é mesmo?! Depois de toda essa explanação sobre vários tipos de ângulos: agudo, obtuso, reto, raso e nulo, um resumo agora cai muito bem.
Então vamos resumir tudo em pouquíssimas palavras:
Resumo sobre os tipos de ângulo
- Ângulo reto é aquele que mede exatamente 90 graus, ou seja: A = 90º
- Ângulo Agudo é aquele cuja medida é maior que 0 grau e menor que 90 graus, ou seja: 0º < A < 90º.
- Ângulo obtuso é aquele cuja medida é maior que 90 graus e menor que 180 graus, ou seja: 90º < A < 180º.
- Ângulo raso ou meia-volta é aquele que mede exatamente 180 graus, ou seja: A = 180º
- Ângulos opostos pelo vértice são aqueles que se encontram em posições opostas em relação ao vértice. Eles são congruentes, pois possuem medidas idênticas.
- Ângulos consecutivos possuem um lado e um vértice em comum.
- Ângulos adjacentes são aqueles dispostos lado a lado e que não possuem pontos internos em comum.
- Ângulos complementares são aqueles que somados resultam em 90º. O complemento de um ângulo é o valor que falta para a soma completar o valor de 90º.
- Ângulos suplementares são aqueles que somados seu valor resulta em 180º. O suplemento de um ângulo é o valor que falta para a soma completar o valor de 180º.
- Ângulos replementares são aqueles que somados resultam em 360º. O replemento de um ângulo é o valor que falta para a soma completar o valor de 360º.
Encerramos aqui a nossa abordagem sobre os ângulos. Saiba que eles são importantíssimos para o estudo das figuras geométricas planas, as quais vamos explicar detalhadamente em breve. Até logo!
Tags
Matemática
Aprende muito acerca do conteúdo d ângulos enriquece o meu conhecimento! Muito obrigada
ResponderExcluirMuito obrigado pelo feed back!
Excluir